Con alforjas

Cualquiera que haya viajado con las alforjas en su bici habrá experimentado unas cuántas sensaciones difíciles de explicar.

Eres autosuficiente, llevas (en teoría) lo necesario para el calor, para el frio la lluvia, material de repuesto para la bici, la cámara de fotos..Por cierto, la primera vez que se viaja de esta manera la alforja va llena de algo de lo necesario y de mucho de lo otro.

Vas de un lado a otro y no contaminas, algo que parece prácticamente imposible en los tiempos que corren.

No tienes prisa, el día es largo. Los pueblos y valles que atraviesas no son como los imaginabas antes de emprender la ruta.

No sabes dónde comerás, ni dónde dormirás al llegar al pueblo que has elegido casi al azar en el mapa esta misma mañana. Y si no llegas al destino, no pasa nada, conocerás otro lugar que probablemente también aparece en el mapa.

Viajar en bici con alforjas es una experiencia que recomiendo a cualquiera que lea estas lineas, incluso al que no las lea.

Desde hace unos cuántos años años 3-4 amigos reservamos una semana en mayo para un viaje de este tipo y he de confesar que, personalmente, son las vacaciones que más me han hecho disfrutar.

Tranquilo, no voy a sacar las fotos de nuestros viajes ni el video de la boda como hace más de un mal amigo. Quería hacer una pequeña introducción del post anterior (De vacaciones) y de los que seguiré colgando en relación a nuestro último viaje por Cantabria, Palencia, Burgos y Euskal Herria. Os preguntaréis que a que viene lo del viaje en un blog de estas características. Buena pregunta. Intentaré encontrar una respuesta a la altura de tan aguda interrogante. En próximos capitulos.

.

De vacaciones

Lumbalgia: dolor de espalda baja, en la zona lumbar, causado por un síndrome músculo-esquelético, es decir, trastornos relacionados con las vértebras lumbares y las estructuras de los tejidos blandos como músculos, ligamentos, nervios y discos intervertebrales.

La definición me vino a la cabeza tras el pinchazo que note de forma súbita en la espalda al agacharme para intentar quitarle la música al desviador del plato. El desagradable tonillo comenzó al cambiar al plato pequeño y se debía al roce de la cadena con el desviador. Y es que era necesario cambiar de plato para afrontar con garantías el primer puerto de nuestro viaje.

Las vacaciones sobre la bici se iban al garete en un momento. La sacudida se me hizo familiar; hace unos meses experimenté la misma sensación (más fuerte) en la misma zona y permanecí varios días con un andar tipo "Chiquito de la calzada".

Habíamos recorrido unos 20 Km desde que salimos de Santillana de Mar (el pueblo de las tres mentiras) y nos encontrábamos en el Mirador de la Vueltuca mirando al bello pueblo de Carmona.

Temía un nuevo latigazo que me dejara fuera de combate. Bajamos hasta Puentenansa y llegó la hora de decidir: seguir el valle del Nansa y subir hacia el puerto de Piedrasluengas o una triste retirada hacia San Vicente de la Barquera para volver a casa en autobús.

Muchos ciclistas me preguntan si la bicicleta es mala para la espalda y en aquel momento recordé lo que habitualmente les contesto: " No es ni buena ni mala, siempre que la postura sea la adecuada y el desarrollo no sea excesivo". Decidí seguir adelante y me propuse adoptar una posición un poco más erguida, utilizar desarrollos muy fáciles aumentando las revoluciones y levantarme del sillín todo lo posible.

Una dosis exacta de Ibuprofeno y la música de Gene Harrys a través de los auriculares del móvil hicieron el resto.

Continuará...

.

* La imagen de Carmona la he localizado en la web. Tenía la moral baja y no estaba para sacar fotos..

Bases físicas de la pedalada. La fuerza (II)

Analicemos el siguiente gráfico. Representa la fuerza ejercida sobre un pedal a medida que gira la biela. La flecha representa la fuerza que ejercemos sobre el pedal, con su módulo en newtons (longitud de la flecha) y su dirección.

Vemos que la fuerza es mínima al principio (0º), aumenta mucho hacia los 90º y disminuye progresivamente hasta desaparecer hacia los 270º. La dirección de dicha fuerza varía también a medida que giramos el pedal.

Bases físicas de la pedalada. La fuerza.

Una cosa tan sencilla como pedalear tiene su miga. La fuerza que transmitimos a los pedales hacen rotar el plato que a su vez tira de la cadena que hace girar el piñón que forma parte de la rueda trasera que también gira y origina el movimiento de la bicicleta y del ciclista que ha aplicado la fuerza que ha sido el origen de esta larga frase. Fuerzas, trabajo, potencia, rozamientos, reacciones, resistencias...pues eso, que tiene miga.

Nos vamos a centrar, para empezar, en la fuerza que aplica el ciclista sobre el pedal, es decir, la madre de todos los corderos.

Para el caso que nos ocupa, la fuerza puede definirse como la acción capaz de modificar el estado de movimiento o de reposo de un cuerpo imprimiéndole una aceleración que modifica el módulo o la dirección de su velocidad o bien, de deformarlo. Es decir, el ciclista aplica una fuerza sobre el pedal, provoca una deformación (mínima) y una aceleración del conjunto pedal-biela.

En física, la fuerza se representa como un vector con su módulo, dirección, sentido y punto de aplicación. Y es que, la fuerza no se ve, aunque veamos sus efectos. Jamás he visto una flecha de color rojo bajo el pedal de ningún ciclista. Pero hace años que al ilustre físico Sr. William Rowan Hamilton se le ocurrió esta brillante idea de los vectores y es el método que vamos a utilizar para explicar todo esto.

En este dibujo vemos que una fuerza que aplicamos en el punto O la podemos descomponer en dos vectores perpendiculares entre si. (Fx y Fy). Quédate con esto porque va a ser muy importante para entender como el ciclista aplica la fuerza sobre el pedal. Por cierto, vamos a medir la fuerza en newtons.

Veamos un ejemplo con tres fuerzas iguales en módulo pero distinta dirección. Son tres fuerzas con los mismos newtons en distintas direcciones y aplicadas en el mismo punto, el pedal.

La intuición (femenina o masculina, intuición al fin y al cabo) nos dice que la fuerza b es la más eficiente en este momento para hacer girar el plato. La explicación que probablemente daremos para razonar nuestra afirmación es que la fuerza b es perpendicular a la biela. Efectivamente, es una razón de peso que intentaremos aclarar con ayuda de la descomposición de los vectores.

En este esquema vemos que la componente perpendicular de los vectores a y c es menor que el vector b. A partir de ahora llamaremos fuerza efectiva a la componente de la fuerza que ejercemos sobre el pedal que es perpendicular a la palanca, la biela en este caso.

Continuará...

Voy a subir el manillar (II)

Vamos a intentar calcular lo que realmente se eleva la potencia sobre la vertical cuando nos animamos a subir la misma. Veamos un primer esquema.

Queremos saber cuanto sube la potencia en el plano vertical si la subimos sobre su eje (ángulo beta). De esta manera conoceremos lo que hemos modificado la diferencia de alturas entre el sillín y el manillar. Vemos que en la posición inicial se crea un triángulo rectángulo que aumenta de tamaño al subir la potencia. Quizá lo veamos más claro en un nuevo esquema en el que eliminamos la bicicleta.

a - longitud inicial de la dirección

a' - longitud de la dirección tras el cambio

b - altura vertical de la potencia al inicio

b' - altura vertical de la potencia tras el cambio

beta- ángulo del tubo de dirección

Queremos conocer por lo tanto el incremento de la altura vertical (b'-b, o sea x) al modificar la

altura de la potencia (a'-a, es decir y). Para ello nos bastaría con estudiar el pequeño triángulo rectángulo que se nos crea arriba, en color azul. El valor "x" corresponde a la hipotenusa (lo que subimos la potencia) y el valor "y" corresponde a uno de los catetos (el valor que queremos calcular) y el ángulo "beta" que hemos definido previamente también vale para este triángulo.

Por lo tanto:

y= x*seno(beta)

Pongamos un ejemplo práctico:

Vamos a subir tres centímetros nuestra potencia y el ángulo del tubo de la dirección de nuestra bicicleta es de 72º.

y = 3 * seno (72º) = 2,85 cm

Es decir, por cada centímetro que subimos nuestra potencia sube 0,95 en la dirección vertical, para un ángulo de 72º. Vamos, prácticamente lo mismo, 0,5 mm menos.

Total, que todo lo que has leído en estos dos últimos artículos se resume en que al subir o bajar la potencia de tu bicicleta, varías casi lo mismo su altura en el eje vertical.

Pues vaya..., te dirás y con razón. Pero ahora quizá puedas lucirte ante tus amigos del club explicando sobre un folio en blanco lo del triangulillo.

Por cierto, prueba a hacer el mismo cálculo para la chopper de la foto del artículo anterior, que calculo tendrá unos 45º de ángulo beta. Verás que eso es otra cosa.

Voy a subir el manillar (I)

Un manillar muy bajo te hará mucho más aerodinámico, ofrecerás menos resistencia al aire e irás más rápido pedaleando lo mismo. Vamos, un chollo. Pero (todos los chollos tienen un pero) la postura que adoptas en la bicicleta no será la más cómoda. No es por animar pero es posible que comiences a notar sobrecargas en la zona lumbar, dolor de cuello, presión y adormecimiento en las manos...

Por cualquiera de estas razones has decidido subir el manillar. Como ocurría al modificar la altura del sillín, al subir el manillar vamos a modificar dos parámetros:

• la diferencia de alturas entre el sillín y el manillar
  
• la distancia sillín-manillar

Debemos tener en cuenta, antes de nada, que subir 1 cm la potencia del manillar no equivale exactamente a disminuir en 1 cm la diferencia de alturas (disminuye algo menos). Por otro lado, la distancia sillín manillar disminuye un poco. Y todo por culpa del ángulo del tubo de dirección, que llamaremos beta

Este ángulo varía de unos modelos de bicicleta a otros y cambia en función de la talla de la bicicleta. Por norma general, a mayor tamaño de cuadro, mayor ángulo (al contrario de lo que ocurría con el ángulo del tubo vertical, como vimos en otro capítulo). En esta tabla se muestran los distintos ángulos del tubo del sillín (alfa) y tubo de la dirección (beta) en función de las distintas tallas de un determinado modelo de bicicleta.

Una bicicleta con un ángulo beta grande será man manejable pero menos estable. Si el ángulo es pequeño, disminuirá la manejabilidad y aumentará la estabilidad. Esta moto es un buen ejemplo de esta última afirmación (ángulo beta muy pequeño).

Las bicicletas que se utilizan en el circo son un claro ejemplo de un elevado ángulo en busca de un fácil manejo. La bicicleta de la imagen inferior tiene un ángulo beta cercano a los 90º.

Continuará...

El fin del retroceso

Prometo dejar de hablar del susodicho tras este post. Al menos voy a intentarlo. Pero para acabar con el tema me veo obligado a aclarar un par de cosas. En el último post (A vueltas con el retroceso ) llegábamos a la conclusión de que utilizando la nueva definición del retroceso, éste no variaba por mucho que adelantásemos o retrasásemos el sillín. Perfecto.

Veamos la siguiente foto.

La posición de la rodilla está retrasada respecto al eje del pedal. Debemos adelantar al ciclista con el fin de mejorar la eficiencia de la pedalada. El ciclista no puede modificar el retroceso ya que, como comentamos, depende del ángulo del tubo del sillín (propio del cuadro) y de la altura del sillín (suponemos que es correcta en este caso).

Pero el ciclista puede adelantar el sillín y aunque no varía el retroceso, sí varía la distancia entre el punto medio y el final del sillín en su parte posterior( la llamamos "m"). Veamos un esquema.

Es la distancia que hemos llamado "m", la que varía al mover el sillín. Es la que definimos y proponemos a nuestros ciclistas. La longitud del sillín no nos importa en este caso. Tampoco el retroceso ya que no se puede modificar.

Consideramos más acertado definir la longitud de "m" que el retroceso considerado desde la punta del sillín. El margen de error es menor y la regulación de la bicicleta será más correcta.

A vueltas con el retroceso

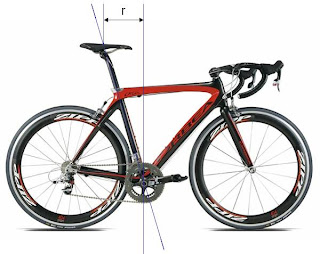Recuerdas que en el último post (El aguafiestas) definíamos el retroceso (r) como la distancia entre una linea imaginaria perpendicular al suelo que pase por el eje del pedalier y el punto del sillín que es atravesado por otra linea imaginaria que siga la dirección del tubo del sillín. Y te quedabas dudando. Y entonces has pensado: "Por mucho que adelante o retrase el sillín, el retroceso permanece invariable. Pues vaya definición de los...retrocesos".

Tienes toda la razón. Si definimos el retroceso de esta manera, este parámetro será propio de cada bicicleta y únicamente variará si modificamos la altura del sillín ( ¿recuerdas?. )
Pero para una misma altura de sillín el retroceso se matiene hagamos lo que hagamos. Y este retroceso dependerá del ángulo del tubo del sillín.

Veamos un ejemplo:

* Una MTB con un ángulo de 70º (BICI A). Se tratará de una bicicleta muy estable, muy adecuada para realizar bajadas ya que el centro de gravedad irá muy retrasado. Puede ser interesante también para subir ya que la rueda trasera soporta gran parte de nuestro peso.

* Otra MTB con un ángulo de 73º, más agresiva, más "echada palante" (BICI B).

Puedes ver que no he modificado en los esquemas el retroceso definido como hasta ahora (distancia horizontal punta del sillín-eje del pedalier).
Lo que ha variado de forma significativa es el retroceso en su nueva definición. La diferencia es de unos 4 cm.
Podemos concluir que el retroceso (definido como al comienzo de este post):

• no varía por mucho que adelantemos o retrasemos el sillín
• varia al aumentar o disminuir la altura del sillín
• la geometría del cuadro va a determinar el retroceso

Continuará.

El aguafiestas

El retroceso del sillín (también llamado avance del sillín) es la distancia horizontal que existe entre la punta de del sillín y una línea imaginaria perpendicular al suelo y que pasa por el eje del pedalier. Esta medida condicionará la eficiencia de la pedalada ya que la fuerza que realiza el pie sobre el pedal varía de una posición a otra, como ya se comentó en otro artículo (KOPS)

Esto que se ve tan bonito en la foto, es algo conplicado de medir. Te han dicho o has leído que en función de tu entrepierna el retroceso de tu bicicleta debe ser 60mm. Para calcular el retroceso actual has tenido que medir con un metro la distancia entre la punta del sillín y la trayectoria de una cuerda con una plomada en su extremo que has hecho coincidir con el eje del pedalier. Para tomar esta medida te has preocupado de que el plano sobre el que se apoya la bici es totalmente horizontal, al igual que la posición del metro a la hora de medir. Después de toda esta operación te das cuenta de que vas algo retrasado y adelantas el sillín 10 mm. Operación finalizada.

Pero como siempre en estos casos, llega el aguafiestas (yo mismo en este caso). Te voy a explicar mis dudas sobre esa modificación que con tanto cariño has realizado sobre tu bicicleta:

• Acabo de visitar la web de una conocida marca italiana de sillines y me he fijado en las longitudes de los sillines. Estas longitudes variaban entre los 255mm y los 293mm. Vamos, casi cuatro centímetros entre el sillín más corto y el más largo. Y claro, entenderéis que nuestra posición sobre la bicicleta será muy distinta con un sillín u otro, aunque en los dos casos el retroceso sea exactamente igual.




• Nuestra posición sobre el sillín está más condicionada por la mitad posterior del sillín (mayor anchura) que por la mitad anterior ya que nuestro apoyo sobre la bicicleta se realiza, sobre todo, en la parte más retrasada. Por lo tanto, con el sillín más corto y más largo únicamente conseguiríamos la misma posición con dos retrocesos distintos, como vemos en el siguiente gráfico. La linea amarilla pasa por el eje del pedalier. El sillín más pequeño exige un retroceso 3cm mayor que el sillín blanco.

Quizá, la solución a este problema sea definir el retroceso como la distancia entre una linea imaginaria perpendicular al suelo que pase por el eje del pedalier y el punto del sillín que es atravesado por otra linea imaginaria que siga la dirección del tubo del sillín. Os propongo una imagen para que nos podamos entender.

Veo que te has quedado pensativo. También esta nueva definición plantea más de una duda. Te dejo. En cuanto tenga tiempo retomamos el tema.
Un saludo.

Sobre las bielas

El conde francés Mede de Sivrac, allá por 1790, no tuvo ningún problema a la hora de elegir la longitud de las bielas para su celerífero. Sobre todo, porque no llevaba bielas. El chisme avanzaba a golpe de pie. Por cierto que debía ser gracioso dar curvas con este aparato.

Concienciado con la importancia que tenía para la salud el trazar curvas , en 1816, un noble alemán diseñó el primer vehículo de dos ruedas con dispositivo de dirección. Esta máquina, denominada draisiana, tenía un manillar que pivotaba sobre el cuadro, permitiendo el giro de la rueda delantera. Al germano tampoco le preocupó la longitud de las bielas ya que su invento tampoco las contemplaba.

En 1839, un herrero escocés, Kirkpatrick Macmillan, añadió las palancas de conducción y pedales a una máquina del tipo de la draisiana. Se trataba de impulsar la máquina con los pies sin tocar el suelo. El mecanismo de impulsión consistía en pedales cortos fijados al cubo de la rueda de atrás y conectados por barras de palancas largas, que se encajaban al cuadro en la parte superior de la máquina. Las barras de conexión se unían a las palancas a casi un tercio de su longitud desde los pedales. La máquina era impulsada por el empuje de los pies hacia abajo y hacia adelante. Seguro que este escocés tuvo que hacer unas cuantas pruebas para calcular la longitud de los pedales y el punto de unión de las palancas sobre los mismos.

A James Starley se le ocurrio fijar unos pedales a la rueda delantera de una bicicleta. Comprobó que cuanto mayor era la rueda mayor era la velocidad que se podía alcanzar y ni corto ni perezoso se calzó una rueda de casi metro y medio de diámetro. Más adelante y con el comienzo de la competición ciclista, se llegaron a fabricar ruedas delanteras de 3 metros de diámetro. Nuevamente creció el peligro para la salud del ciclista en forma de severos castañazos. Las bielas de la Penny-farthing (así se llamó porque la asimetría de las ruedas se asemejaba a dos monedas de diferente tamaño) estarían diseñadas para poder impulsar la bicicleta y alcanzarlas cómodamente con los pies. En este video de youtube podéis ver a un personaje montando este tipo de bicicleta.

Los pedales y las bielas que conocemos en la actualidad los utilizó en 1885 John Kemp Starley en su “bicicleta de seguridad”, que gracias al uso de los rodamientos se propulsaba mediante una cadena. Tuvo además el bonito detalle de acoplar frenos en la rueda delantera aportando una ayuda inestimable a la prevención de la salud.

En realidad hoy tenía pensado hablar sobre las bielas, como bien dice el título del artículo. Pero claro, te lías, te lías y pasa lo que pasa. Un consejo: no busquéis nada en wikipedia. . Terminas sin recordar lo que buscabas. Lo digo por experiencia.

Cambio en la altura del sillín

Tus amigos del club cicloturista te han dicho que vas muy bajo sobre tu bicicleta, que no estiras lo suficiente la rodilla y que deberías subir el sillín. Al final, te animas y decides aumentar la altura de tu sillín. Pero, espera. Quieto. Antes de coger la allen debes tener en cuenta un par de cosas. Por cierto quizá no sepas que originalmente Allen era una marca registrada de Allen Manufacturing Company en Hartford, Connecticut en 1943, empresa dedicada a fabricar este tipo de herramientas. Pero debéis tener muy presente que la companía Bauer & Schaurte Karcher en Neuss, Alemania, fue el que realmente inventó este inteligente sistema para atornillar y desatornillas tornillos. Por eso ese sistema se conoce en muchas partes del Mundo como Inbus (Innensechskantschraube Bauer und Schaurte).

Estabamos con el tema del sillín y te disponías a subirlo. Al realizar esta sencilla maniobra vas a modificar, además de la altura del sillín, otros dos parámetros: el retroceso y la distancia sillín-manillar. Y todo por culpa del el ángulo del tubo vertical que, como ya dijimos, tiene muy poco de vertical.

Experimento

Observa estos dos esquemas. En el primero de ellos la altura del sillín es de 710mm y en el segundo esquema de 740mm (podréis pensar que subir un sillín 3 cm es mucho subir, pero me interesa que sea así en este caso para que todo lo que estoy contando sea más evidente). El ángulo del tubo del sillín es de 73,5º en ambos casos.

Después de hacer los esquemas me he dado cuenta que la distancia entre la raya blanca y la naranja parece igual. Os aseguro que no es así. En el esquema de abajo, la distancia (el retroceso del sillín) es mayor. Tendréis que creerme.

Nos centramos en el retroceso (r) y en cómo se modifica al cambiar la altura del sillín. Debemos estudiar el triángulo que forman el eje del pedalier, el punto medio del sillín y el punto de cruce entre una horizontal que pase por el punto medio del sillín y una vertical que pase por el eje del pedalier.
Planteemos el problema:

• Conocemos a (altura del sillín)
• Sabemos el ángulo del tubo del sillín (73,5º habitualmente) y podemos calcular el complementario (x), que es realmente el que nos va a interesar (90º-73,5º)
• Queremos conocer el retroceso r
  
  
  

Si sabéis algo de trigonometría conoceréis esta fórmula:

r=a*seno(x)

En el ejemplo anterior: r=710* seno(90º-73,5º)= 201

Y si subo 3 cm el sillín: r=740* seno(90º-73,5º)= 210

Es decir, con la nueva altura, el sillín se ha retrasado 9mm, practicamente 1 cm.

Conclusiones:

• Por cada centímetro que subamos o bajemos el sillín lo retrasamos o adelantamos 3mm (para un ángulo de 73,5º).
• A mayor ángulo del tubo del sillín, menos lo retrasamos al subirlo y viceversa. En tubo del sillín que fuese totalmente vertical el retroceso no se modificaría por mucho que meneásemos el sillín.
• Los esquemas hay que hacerlos con más cuidado si realmente queremos que sirvan para algo
  

Observación

Si os animáis ha realizar estos cálculos en una hoja Excel debéis tener en cuenta que al utilizar la fórmula del seno el ángulo debe expresarse en radianes (360º=2π radianes). Por comentar.